Copy this code and paste it into a new quarto document in R. We will be using quarto for assignments, it is good to practice using it with each workshop.

tidyr

By the phrase tidy data, it is meant the preferred way of arranging data that is easy to analyse. The principles of tidy data are:

  • Each variable forms a column.
  • Each observation forms a row.
  • Each type of observational unit forms a table.

Introduction to the tidyverse

We will be largely using the tidyverse suite of packages for data organisation, summarizing, and plotting; see https://www.tidyverse.org/.

Let’s load that package now: Remember if you have not installed it you will need to use install.packages() first. We installed it in the first workshop so you can return to that code to see how we did it.

Code 
library(tidyverse)

Dataset

For this workshop we will use some tidyverse built in datasets. Each dataset below shows the same values of four variables: country, year, population, and number of documented cases of TB (tuberculosis), but each dataset organizes the values in a different way. Take a look at these datasets by typing their names into a code chunk or directly into the console. You can also try your hand at the functions head() and summary().

Code 
table1
# A tibble: 6 × 4
  country      year  cases population
  <chr>       <dbl>  <dbl>      <dbl>
1 Afghanistan  1999    745   19987071
2 Afghanistan  2000   2666   20595360
3 Brazil       1999  37737  172006362
4 Brazil       2000  80488  174504898
5 China        1999 212258 1272915272
6 China        2000 213766 1280428583
Code 
table2
# A tibble: 12 × 4
   country      year type            count
   <chr>       <dbl> <chr>           <dbl>
 1 Afghanistan  1999 cases             745
 2 Afghanistan  1999 population   19987071
 3 Afghanistan  2000 cases            2666
 4 Afghanistan  2000 population   20595360
 5 Brazil       1999 cases           37737
 6 Brazil       1999 population  172006362
 7 Brazil       2000 cases           80488
 8 Brazil       2000 population  174504898
 9 China        1999 cases          212258
10 China        1999 population 1272915272
11 China        2000 cases          213766
12 China        2000 population 1280428583
Code 
table3
# A tibble: 6 × 3
  country      year rate             
  <chr>       <dbl> <chr>            
1 Afghanistan  1999 745/19987071     
2 Afghanistan  2000 2666/20595360    
3 Brazil       1999 37737/172006362  
4 Brazil       2000 80488/174504898  
5 China        1999 212258/1272915272
6 China        2000 213766/1280428583

Exercise 1.1

For each of the sample tables, describe what each observation and each column represents. Which is the most tidy?

Piping

Tip

The piping operation is a fundamental aspect of computer programming. The semantics of pipes is taking the output from the left-hand side and passing it as input to the right-hand side.

The R package magrittr introduced the pipe operator %>% and can be pronounced as “then”. In RStudio windows/Linux versions, press Ctrl+Shift+M to insert the pipe operator. On a Mac, use Cmd+Shift+M.

R also has its own pipe, |>, which is an alternative to %>%. You will see both used in this course. If you want to change the pipe inserted automatically with Ctrl+Shift+M, find on the menu Tools > Global Options, then click on Code and check the box that says “Use Native Pipe Operator”.

Consider the study guide dataset rangitikei.csv (Recreational Use of the Rangitikei river). The first 10 rows of this dataset are shown below:

   id loc time w.e cl wind temp river people vehicle
1   1   1    2   1  1    2    2     1     37      15
2   2   1    1   1  1    2    1     2     23       6
3   3   1    2   1  1    2    2     3     87      31
4   4   2    2   1  1    2    1     1     86      27
5   5   2    1   1  1    2    2     2     19       2
6   6   2    2   1  2    1    3     3    136      23
7   7   1    2   2  2    2    2     3     14       8
8   8   1    2   1  2    2    2     3     67      26
9   9   1    1   2  1    3    1     2      4       3
10 10   2    2   1  2    2    2     3    127      45

Try the following examples after loading the rangitikei dataset.

select()

Code 
new.data <- rangitikei |> 
  select(people, vehicle)

names(new.data)
[1] "people"  "vehicle"

What does select() do?

Code 
rangitikei |> 
  select(people, vehicle) |> # select columns
  ggplot() + # make a plot using those columns
  aes(x=people, y=vehicle) + 
  geom_point()

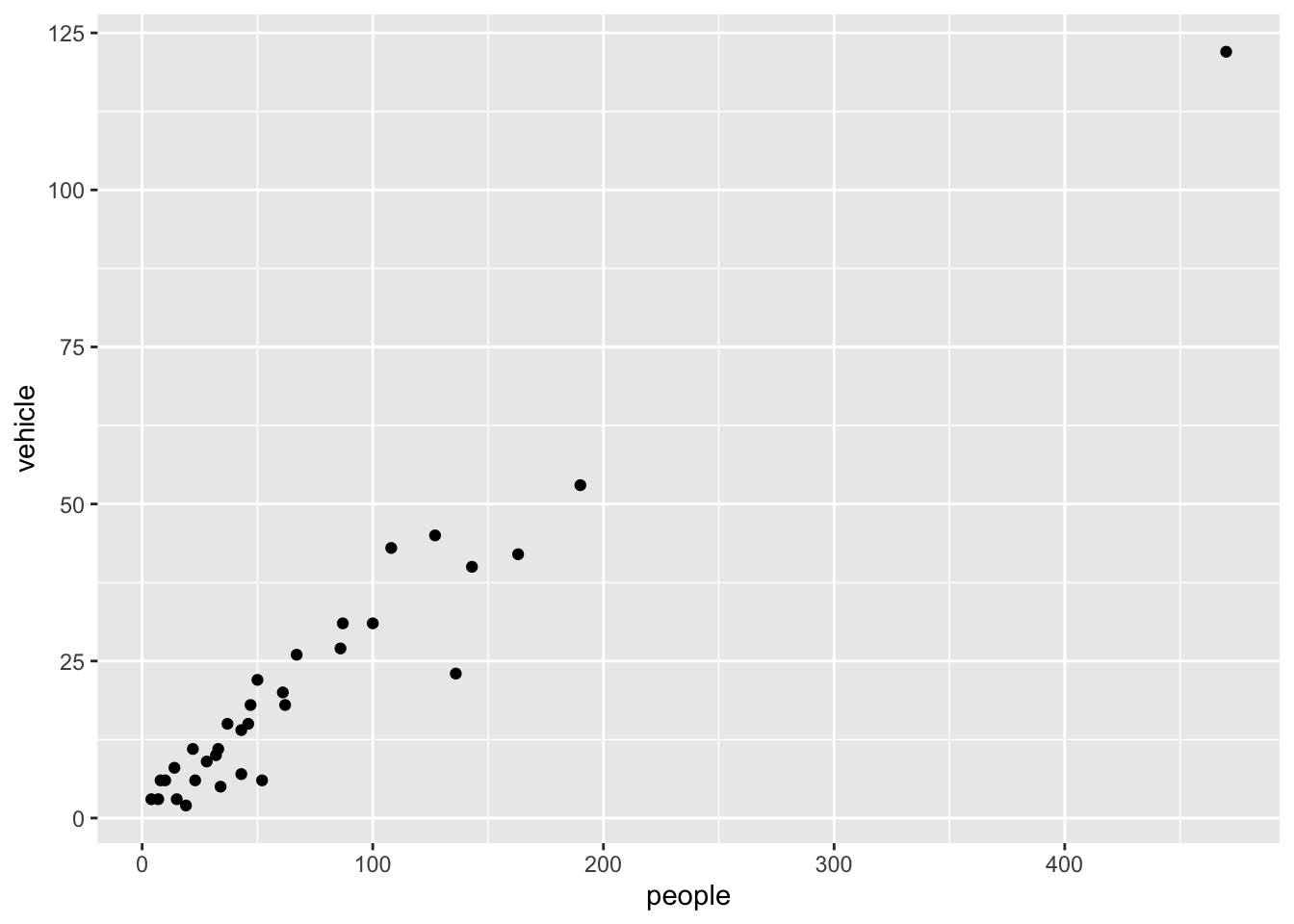
We select two columns and create a scatter plot with the above commands.

Now try another function:

filter()

Code 
rangitikei |> 
  filter(wind==1) |> 
  select(people, vehicle) |> 
  ggplot() +
  aes(x=people, y=vehicle) +
  geom_point()

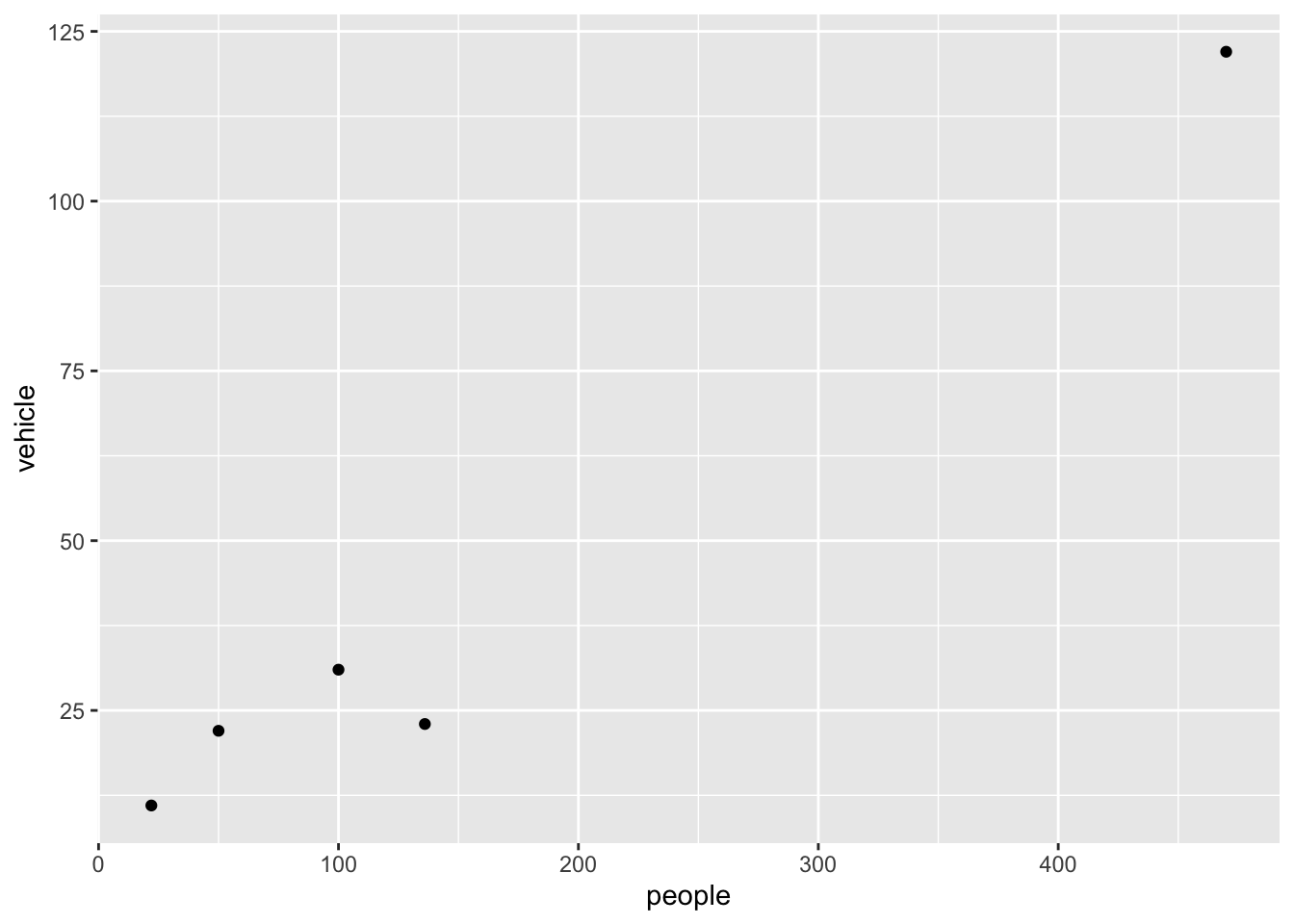
What does filter() do?

The above commands filter the data for the low wind days and plots vehicle against people. filter() subsets the data for all observations matching a specified criteria.

arrange()

Code 
rangitikei |> 
  filter(wind==1) |> 
  arrange(w.e) |> 
  select(w.e, people, vehicle)
  w.e people vehicle
1   1    136      23
2   1     50      22
3   1    100      31
4   1    470     122
5   2     22      11

mutate()

Assume that a $10 levy is collected for each vehicle. We can create this new levy column as follows.

Code 
rangitikei |> 
  mutate(levy = vehicle*10) |> 
  select(people, levy) |> 
  ggplot() +
  aes(x = people, y=levy) +
  geom_point()

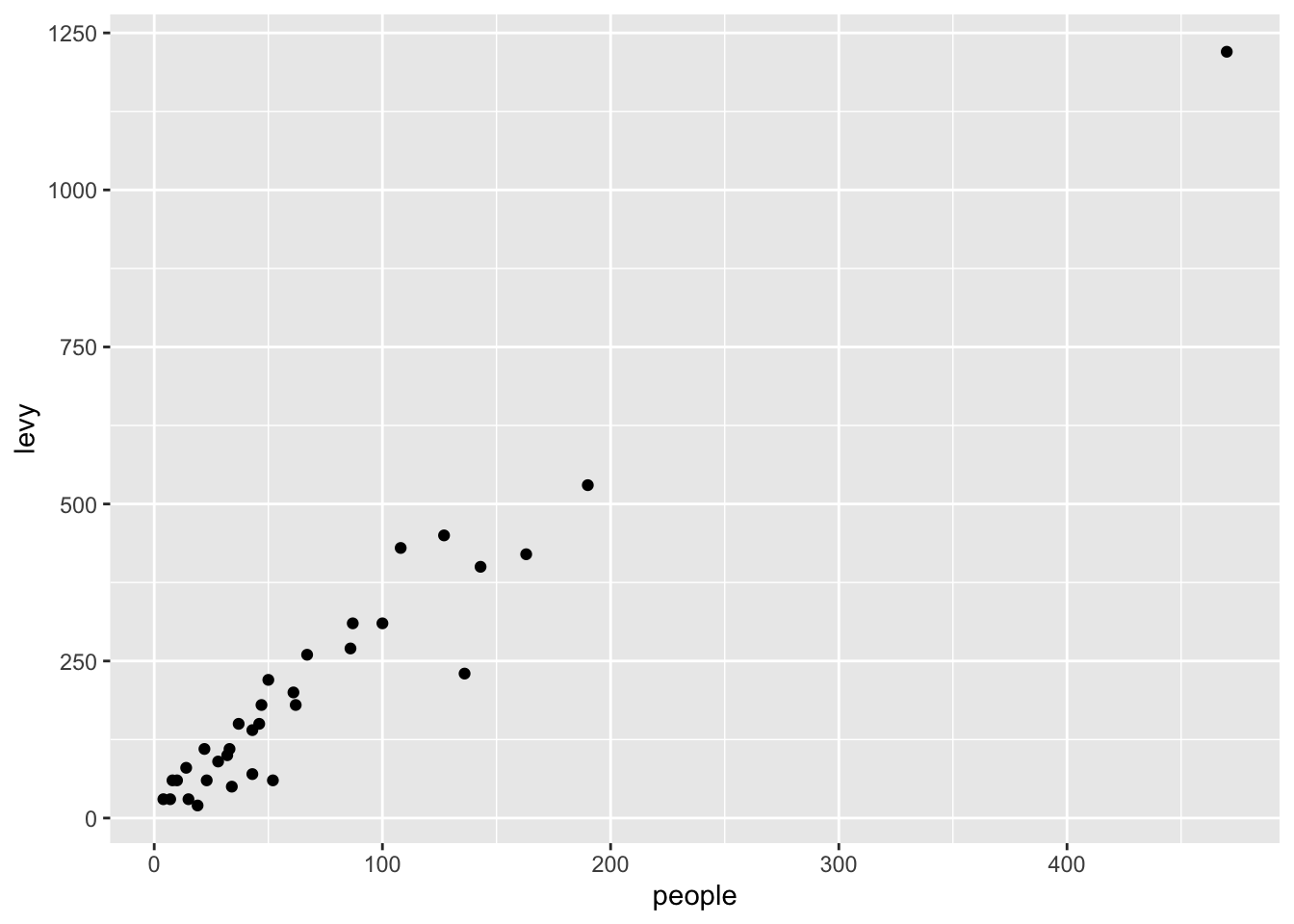
Note that the pipe operation was used to create a scatter plot using the newly created column.

summarise()

Code 
rangitikei |> 
  summarise(total = n(), 
            avg = mean(people)
            )
  total      avg
1    33 71.72727

We obtain the selected summary measures namely the total and the mean number of people. Try-

Code 
rangitikei |> 
  filter(wind == 1) |> 
  summarise(total = n(), 
            avg = mean(people)
            )
  total   avg
1     5 155.6

group_by()

We obtain the wind group-wise summaries below:

Code 
rangitikei |> 
  group_by(wind) |> 
  summarise(total=n(), 
            avg=mean(people))
# A tibble: 3 × 3
   wind total   avg
  <int> <int> <dbl>
1     1     5 156. 
2     2    26  59.7
3     3     2  19

There are many more commands such as the transmute function which conserves only the needed columns. Try

Code 
rangitikei |> 
  group_by(wind, w.e) |> 
  transmute(total=n(), 
            avg=mean(people))
# A tibble: 33 × 4
# Groups:   wind, w.e [6]
    wind   w.e total   avg
   <int> <int> <int> <dbl>
 1     2     1    18  72.1
 2     2     1    18  72.1
 3     2     1    18  72.1
 4     2     1    18  72.1
 5     2     1    18  72.1
 6     1     1     4 189  
 7     2     2     8  31.8
 8     2     1    18  72.1
 9     3     2     1   4  
10     2     1    18  72.1
# ℹ 23 more rows

A simple frequency table is found using count(). Try-

Code 
rangitikei |> 
  group_by(wind, w.e) |> 
  count(temp)
# A tibble: 10 × 4
# Groups:   wind, w.e [6]
    wind   w.e  temp     n
   <int> <int> <int> <int>
 1     1     1     1     1
 2     1     1     3     3
 3     1     2     3     1
 4     2     1     1     4
 5     2     1     2    12
 6     2     1     3     2
 7     2     2     2     6
 8     2     2     3     2
 9     3     1     2     1
10     3     2     1     1
Code 
rangitikei |> 
  group_by(wind, w.e) |> 
  count(temp, river)
# A tibble: 16 × 5
# Groups:   wind, w.e [6]
    wind   w.e  temp river     n
   <int> <int> <int> <int> <int>
 1     1     1     1     1     1
 2     1     1     3     3     3
 3     1     2     3     3     1
 4     2     1     1     1     1
 5     2     1     1     2     1
 6     2     1     1     3     2
 7     2     1     2     1     3
 8     2     1     2     2     2
 9     2     1     2     3     7
10     2     1     3     3     2
11     2     2     2     1     2
12     2     2     2     3     4
13     2     2     3     2     1
14     2     2     3     3     1
15     3     1     2     2     1
16     3     2     1     2     1

The count() is useful to check the balanced nature of the data when many subgroups are involved.

Exercise 1.2

Generate a summary table to show the average number of people observed at each of the three rivers.

Code 
# your code goes here

Exercise 1.3

Generate a summary table to show the average number of vehicles observed at each of the three wind levels.

Code 
# your code goes here

Exercise 1.4

Repeat the above exercise 1.2 but now calculate the median number of people and the median number of vehicles at each river in a single table.

Code 
# your code goes here

Exercise 1.5

Use the above three tables you generate to describe the Rangitikei dataset. What other information or tables might be useful?

Now let’s practice using these functions using the TB data.

Exercise 1.6

Using table1, compute rate of TB cases per 10,000 and the total cases per year

Code 
# your code goes here

Exercise 1.7

Generate a summary table to show the total cases in each country. Your table should have 3 rows.

Code 
# your code goes here

Exercise 1.8

For table2, write pseudo-code for how you would perform the following actions. Sketch/describe how you would do these.

  1. Extract the number of TB cases per country per year.
  1. Extract the matching population per country per year.
  1. Divide cases by population, and multiply by 10000.
  1. Store back in the appropriate place.

Exercise 1.9

What does na.rm = TRUE do in the functions mean() and sum()?

Code 
# your code goes here

Exercise 1.10

What does the function na.omit() do? Why would you add it to a piping sequence of code when tidying data?

Code 
# your code goes here